Question

I want to know the coefficient of each expression and all it’s potential roots

Answer 1

We are given the following polynomial

`3x^5-7x^4-5x^3+18x^2-5`

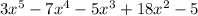
The constant term is -5

The factors of the constant term are ±1 and ±5

The leading coefficient is 3

The factors of the leading coefficient are ±1 and ±3

We can use the factors of the constant term and the leading coefficient to find the potential roots

`potential\; roots=(p)/(q)`

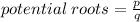
Where p represents the factors of the constant term and q represents factors of the leading coefficient.

`\begin{gathered} (p)/(q)=(\pm1,\pm5)/(\pm1,\pm3) \\ (p)/(q)=(\pm1)/(\pm1),(\pm1)/(\pm3),(\pm5)/(\pm1),(\pm5)/(\pm3) \\ (p)/(q)=\pm1,\pm(1)/(3),\pm5,\pm(5)/(3) \end{gathered}`

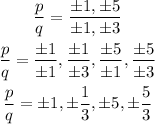
Therefore, the potential roots of the given polynomial are

`\pm1,\pm(1)/(3),\pm5,\pm(5)/(3)`