Question

4: Using the model, what will the population of the city be when it is 25 years old? Round your answer to the nearest hundred. You must find the exponential regression equation first.

Answer 1

Using an Exponential regression Calculator

we have that

Give me a few minutes to complete the regression

`y=30,056.97\left(1.06\right)^x`

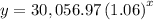
so

For x=25 years

substitute

`\begin{gathered} y=30,056.97\left(1.06\right)^(25) \\ y=129,000 \end{gathered}`

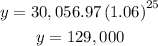
Part 2

Using an exponential equation of the form

`y=a(e)^(bx)`

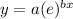
Using an Exponential regression Calculator

we have that

Give me a few minutes to complete the regression

the equation is

`y=30,056.97(e)^(0.06x)`

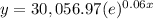
For x=25 years

substitute

`\begin{gathered} y=30,056.97(e)^(0.06(25)) \\ y=134,706 \end{gathered}`

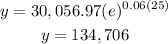
The answer is option B