To solve the exercise let's remember that the volume of a cone is equal to
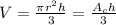
Where r is de radius and h is the height. Note that Ac is the circle's base of the cone. Solving the equation as a function of the height and replacing the information we have from the exercise
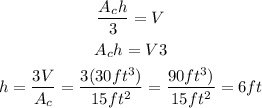
Thus, the height of the cone is 6 ft.The correct answer is D.