Question

A principal of $1500 is invested at 9% interest, compounded annually. How many years will it take to accumulate $4000 or more in the account? (Use the calculator provided if necessary.)Write the smallest possible whole number answer.

Answer 1

Step-by-step explanation

The equation of the compounded interest is the following:

`Interest\text{ Earned=Principal\lparen1+}(r)/(n)\text{\rparen}^(nt)`

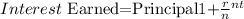
Where P=Principal=1500, r=rate=0.09, n = number of times interest rate is compounded = 1, t=time=unknown value

Plugging in the terms into the expression:

`4000=1500(1+(0.09)/(1))^t`

`\mathrm{Switch\:sides}`

`1500\left(1+(0.09)/(1)\right)^t=4000`

`\mathrm{Divide\:both\:sides\:by\:}1500`

`(1500\left(1+(0.09)/(1)\right)^t)/(1500)=(4000)/(1500)`

`\mathrm{Simplify}`

`\left(1+(0.09)/(1)\right)^t=(8)/(3)`

`\mathrm{If\:}f\left(x\right)=g\left(x\right)\mathrm{,\:then\:}\ln \left(f\left(x\right)\right)=\ln \left(g\left(x\right)\right)`

`\ln \left(\left(1+(0.09)/(1)\right)^t\right)=\ln \left((8)/(3)\right)`

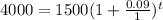
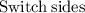
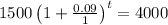
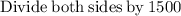
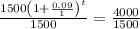
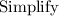
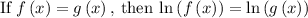
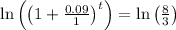
Apply log rule:

`t\ln \left(1+(0.09)/(1)\right)=\ln \left((8)/(3)\right)`

`\mathrm{Divide\:both\:sides\:by\:}\ln \left(1.09\right)`

`(t\ln \left(1.09\right))/(\ln \left(1.09\right))=(\ln \left((8)/(3)\right))/(\ln \left(1.09\right))`

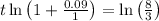
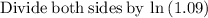
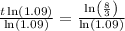
Simplify:

`t=(\ln \left((8)/(3)\right))/(\ln \left(1.09\right))`

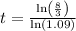
Expressing as a decimal:

`t=11.38`

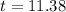
In conclusion, we will need 11 years to accumulate $4,000