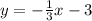Given:
Line p contains the point (6,- 5 and is perpendicular to line q the equation for line q is y=3x+5 the slope of line q is 3. and the slope of line p is -1/3. Equation for line p in point-slope form is y = -1/3x - 3.
Required:
Write an equation for line p in slope-intercept form.
Step-by-step explanation:
The equation of line q is:
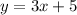
The line p is perpendicular to line q.
The slope of line q = 3
We know that the perpendicular line has negative reciprocal slopes.
So the slope of line p
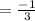
The equation of line has slope m and passes through from one point is given as:

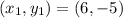
Thus the equation of line p is:

Final Answer:
The equation of line p is: