Given data:
Principal (starting amount) = $10, 000
Interest rate compounded quarterly = 3.6% = 0.036
The modeled account balance is
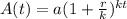
SOLUTION A.
The values that should be used for a, r and k are:
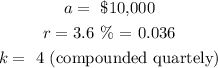
SOLUTION B
The money Hailey will have in the account in 9 years would mean that t = 9 years. Hence,

SOLUTION C
The annual percentage yield (APY) can be calculated using the formula below
