Question

NASA launches a rocket at t= 0 seconds. It's height, in meters above sea level, as a function of time is given by h(t) = -4.9t^2 + 238t + 122.

Answer 1

Given the function:

`h(t)=-4.9t^2+238t+122`

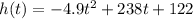
Where h is the height of the rocket and t is the time in seconds

The rocket launches at t = 0

so, to find the height substitute with t = 0 into the function

so, the height =

`-4.9\cdot0+238\cdot0+122=122`

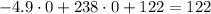
so, the answer will be when t = 0 , h(t) = 122

How long will the rocket remain in the air ?

So, we will find the value of t when h(t) = 0

`\begin{gathered} -4.9t^2+238t+122=0 \\ a=-4.9,b=238,c=122 \\ \\ t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}=\frac{-238\pm\sqrt[]{238^2-4\cdot-4.9\cdot122}}{2\cdot-4.9} \\ \\ t=-0.507,\text{ or t = 49.0787} \end{gathered}`