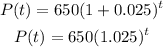Answer:
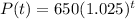
Explanations:
The initial population of quail be represented as P₀
P₀ = 650
Annual increase rate, r = 2.5% = 2.5/100 = 0.025
The exponential function that models the population will be given by the formula:
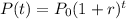
Substitute P₀ and r into the equation above: