To solve this question we will use the following diagram:
Therefore:
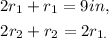
Adding like terms in the above equations we get:
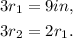
Therefore:
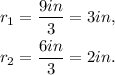
Now, notice that the orange region is formed by 2 semicircles of radius 3in and 2 semicircles of radius 1in, then, the area is:
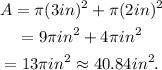
Answer: 40.84in².