Question

While writing a paper on making decisions in groups, Peter researched the number of members on a variety of committees. Number of members Number of committees 26 4 44 2 93 1 96 3 X is the number of members that a randomly chosen committee has. What is the expected value o Write your answer as a decimal.

Answer 1

The expected value formula would come in handy, it is

`Expected-value=\Sigma\text{ xP(x)}`

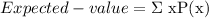
Step 1

Total number of committee = 4 + 2 + 1 +3 = 10

Step 2

probality of picking of (26) = 4/10

probality of picking of (44) = 2/10

probality of picking of (93) = 1/10

probality of picking of (96) = 3/10

`\begin{gathered} \text{Expected Value = }(4)/(10)*26\text{ + }(2)/(10)*\text{ 44 + }(1)/(10)*93\text{ + }(3)/(10)*\text{ 96 } \\ \text{ = }(104)/(10)\text{ +}(88)/(10)\text{ + }(93)/(10)\text{ + }(288)/(10) \\ \text{ = 10.4 + 8.8 + 9.3 + 28.8} \\ \text{ = 57.3} \end{gathered}`

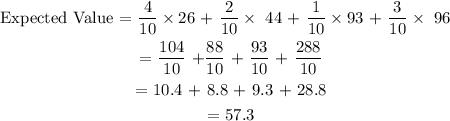
Therefore expected value = 57.3