The given equation is
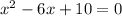
First, we subtract 10 from each side
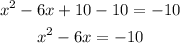
Then, we divide the linear coefficient by half and elevated it to the square power.
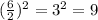
Then, we add 9 on each side.
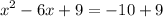
Now, we factor the trinomial.
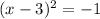
At this point, we can deduct that the equation has no real solutions because there's no real number whose square power ends up in a negative number.
Hence, the equation has no solutions.