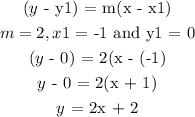ANSWER
The equation of the line that passes through (-1, 0) is y = 2x + 2
Explanation
Given information
The given points on the graph are (-1, 0) and (0, 2)
From the given points, we can deduce the below data
x1 = -1
y1 = 0
x2 = 0
y2 = 2
The next step is to find the slope between the two points
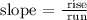
Where
rise = y2 - y1
run = x2 - x1
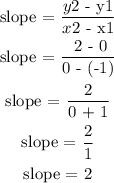
From the above equation, you will see that the slope between the two lines is 2
The next process is to find the equation of the line that passes through (-1, 0)
Recall that,
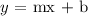
where,
m is the slope of the line
b is the intercept of the y-axis
For a given point, we will be using the formula below