Question

The students government wants to sell m magazine to make a profit of at least $3,000. They make $1.25 per m subscription sold.Their only expense were for advertising of $100 in school and $150 in community. write a linear inequality model for this problem

Answer 1

They want to make a profit of $3,000.

Their income is $1.25 per subscription. Then, the total income is 1.25x, being x the number of subscriptions.

Their expenses are fixed (that is, they do not depend on the number of subscriptions) and are $100 and $150, a total of $250.

Then, we can write the equation for the profit P in function of the number of subscriptions as:

`P=1.25x-250`

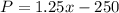
If profit needs to be larger than $3000, we can write:

`\begin{gathered} P>3000 \\ 1.25x-250>3000 \end{gathered}`

And solve:

`\begin{gathered} 1.25x-250>3000 \\ 1.25x>3000+250 \\ 1.25x>3250 \\ x>(3250)/(1.25) \\ x>2600 \end{gathered}`

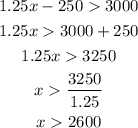
They need at least 2600 subscriptions to make $3000 in proft.