Question

Select the correct answer from each drop-down menu.Consider this equation.(40)}I- 0The first step in solving this equation is to. The second step is toSolving this equation for x initially yields• Checking the solutions shows that

Answer 1

Step-by-step explanation:

Given:

`(4x)^{(1)/(3)}\text{ - x = 0}`

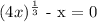
To find:

the steps in solving the expression and the value(s) of x

To determine the value of x, first, we will add x to both sides:

`\begin{gathered} (4x)^{(1)/(3)}\text{ -x + x = 0 + x} \\ (4x)\placeholder{⬚}^{(1)/(3)}\text{ }=\text{ x} \end{gathered}`

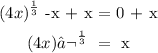
Next, cube both sides of the equation:

`\begin{gathered} ((4x)^{(1)/(3)})^3\text{ = x}^3 \\ ((4x)^{(3)/(3)})^\text{ = x}^3 \\ 4x\text{ = x}^3 \end{gathered}`

Lastly, solve for x to determine the number of solutions:

`\begin{gathered} subtract\text{ 4x from both sides:} \\ x^3\text{ - 4x = 0} \\ x(x^2\text{ - 4\rparen = 0} \\ x\text{ = 0 or x}^2-4\text{ = 0} \\ \\ x^2\text{ - 4 = 0} \\ x^2\text{ = 4} \\ x\text{ = }\pm√(4) \\ x\text{ = }\pm2 \\ \\ The\text{ values of x = -2, 0, 2} \end{gathered}`

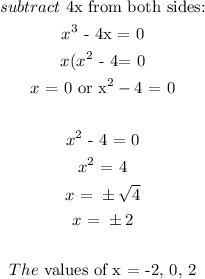
The first step in solving the equation is to add x to both sides. The second step is to cube both sides.

Solving this equation for x initially yields 3 possible solutions. Checking the solutions shows