Question

Use the discriminant, b^2 - 4ac, to determine the number of solutions of the following quadratic equation. -3y^2 + y = - 5Then solve the quadratic equation using the formula Y = (Formula to use is in the pic attached)

Answer 1

The quadratic we are working with is;

`-3y^2+y=-5`

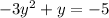
We can rewrite the equation in standard form as;

`-3y^2+y+5=0`

Comparing this with the standard form of a quadratic equation, we see that ;

a = -3 , b = 1 and c =5.

The discriminant from the solution formula is;

`\begin{gathered} b^2-4ac,\text{ here , b =1 and c =5, thus;} \\ b^2-4ac=(1)^2-4(-3(5)) \\ =1-4(-15) \\ =1+60 \\ =61 \end{gathered}`

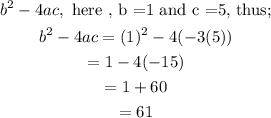
The discriminant is positive, therefore, there are 2 different real solutions to this quadratic equation.

Let us obtain these solutions, using the full quadratic formula;

`y=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Let's insert the values of a, b and c to obtain;

`\begin{gathered} y=\frac{-1\pm\sqrt[]{61}}{-6} \\ y=\frac{-1+\sqrt[]{61}}{-6}\text{ and }\frac{-1-\sqrt[]{61}}{-6} \\ \text{simplified as} \\ y=\frac{1-\sqrt[]{61}}{6}\text{ and }\frac{1+\sqrt[]{61}}{6} \end{gathered}`

Therefore, these are the solutions for y.