In order to simplify the expression, let's divide each term in the numerator by the denominator:
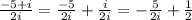
Then, to remove the complex number i from the denominator of the first fraction, let's multiply the numerator and denominator by i:
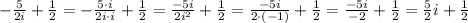
Therefore the complex number in the form a + bi is equal to 1/2 + (5/2)i.