Let x be the pounds of 45% copper alloy
Let y be the pounds of 69% copper alloy
To get the amount of copper in a alloy you multiply the pounds of it by the % of copper in decimal form.
Use 0.45x and 0.69y to get a alloy of 42*0.66 (42 pounds containig 66% copper)
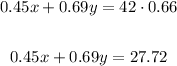
x and y needs to sum the pounds in the last alloy:
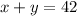
Use the next system of equations to solve the given problem:
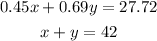
1. Solve y in the second equation:
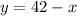
2. Substitute the y in the first equation by the value you get in first step:
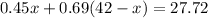
3. Solve x:
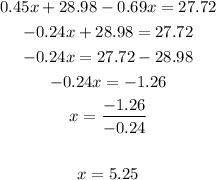
4. Use the value of x to solve y:
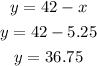
Solution: x=5.25, y=36.75
Then, the metallurgist must use 5.25 pounds of the alloy containing 45% copper and 36.75 pounds of the alloy containing 69% copper