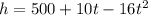Question

a family is 500 feet above the ground in the basket of a hot-air balloon in ascending at the consistent rate shown.Adele hello and someone accidentally dropped a penny out of the balloon write a model for height h,p of the penny t seconds after the penny dropped

Answer 1

A model for height h of the penny t seconds after the penny dropped ​is;

`h=500+10t-16t^2`

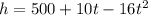
Step-by-step explanation:

Given that the penny was dropped from a hot-air balloon that moves at a constant rate of;

`u_0=10ft\text{/s}`

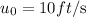
Note that the penny will also have the same initial rate.

At the point when the penny was dropped they are already at height;

`h_0=500ft`

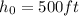
The gravitational pull on the penny (acceleration due to gravity);

`a=-32ft/s^2`

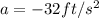
The height of the penny at time seconds after it was dropped can be modelled using the equation of motion;

`h=h_0+u_0t+(1)/(2)at^2_{}_{}^{}`

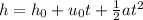
Where;

`\begin{gathered} h_0=initial\text{ height} \\ u_0t=height\text{ covered by initial velocity} \\ (1)/(2)at^2=height\text{ covered by gravitational pull} \end{gathered}`

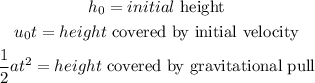
Substituting the given values we have;

`\begin{gathered} h=h_0+u_0t+(1)/(2)at^2_{} \\ h=500+10t+(1)/(2)(-32)t^2 \\ h=500+10t-(32)/(2)t^2 \\ h=500+10t-16t^2 \end{gathered}`

Therefore, a model for height h of the penny t seconds after the penny dropped ​is;

`h=500+10t-16t^2`