Question

According to the poll conducted by Khalid corporation in March 2011 the metropolitan area with the highest and lowest proportion of obese adults were Evansville, IN-KY, boulder Colorado retrospectively.for every 311 people who were not obese there were 189 who were. In Boulder for every 16 obese people there were 109 who were not obese. At that time the estimated population were 358,676 for Evansville and 303, 482 for Boulder how many more obese people were there in Evansville than Boulder.

Answer 1

Step-by-step explanation:

We are given the ratios of obese to non-obese adults in two cities.

To simplify our calculations and explanations we shall assign variables to obese and non-obese adults as follows;

`\begin{gathered} x=obese \\ y=non-obese \end{gathered}`

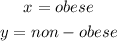
That means the ratios for the two cities would be as shown below;

`\begin{gathered} Evansville=x:y \\ Evansville=189:311 \end{gathered}`

`\begin{gathered} Boulder=x:y \\ Boulder=16:109 \end{gathered}`

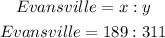
With the given ratios we can now calculate the number out of the entire population which is represented by each variable.

This is shown below;

`\begin{gathered} Evansville: \\ Total=358,676 \\ x=(189)/((189+311))*358676 \end{gathered}`

`\begin{gathered} x=(189)/(500)*358676 \\ \end{gathered}`

`x=135579.528`

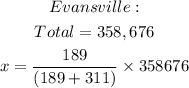
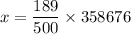
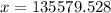
We can round this to the nearest whole number which is;

`x\approx135,580`

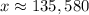
The value of y for Evansville would now be;

`\begin{gathered} Total-x=y \\ 358676-135580=y \end{gathered}`

`y=223,096`

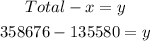
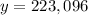
This means in Evansville, there are 135,580 obese adults and 223,096 non-obese adults. We shall now move on to Boulder;

`\begin{gathered} Boulder: \\ Total=308,482 \\ x=(16)/((16+109))*308482 \end{gathered}`

`x=(16)/(125)*308482`

`x=39485.656`

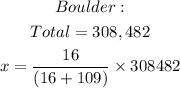
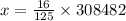
We will round this to the nearest whole number and that is;

`x\approx39,486`

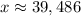
The value of y in Boulder will now be;

`\begin{gathered} Total-x=y \\ 308482-39486=y \end{gathered}`

`y=268,996`

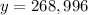
With this result for Boulder, we can conclude that there are 39,486 obese adults and 268,996 non-obese adults in Boulder.

The number of obese people compared for both cities are;

`\begin{gathered} Obese\text{ }people: \\ Evansville=135,580 \\ Boulder=39,486 \end{gathered}`

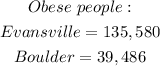
The difference would be;

`\begin{gathered} Difference=135580-39486 \\ Difference=96,094 \end{gathered}`

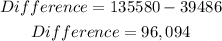
ANSWER:

There were 96,094 more obese people in Evansville than in Boulder