Question

consider abc whose vertices are a(2,1) , b (3,3), and c (1,6); let line segment ac represent the base of the triangle use the distance formula to find the length of the base and the height of abc

Answer 1

Given:

`\begin{gathered} A(2,1),B(3,3),C(1,6) \\ AC\text{ is the base of the triangle} \end{gathered}`

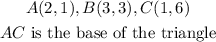
The sketch of triangle ABC can be shown below;

Let M be the midpoint of line segment AC.

To get the length of the base AC;

Using the distance between two points formula;

`\begin{gathered} d=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ \text{where;} \\ x_1=2 \\ x_2=1 \\ y_1=1 \\ y_2=6 \\ \\ \text{Hence, } \\ d=AC=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ AC=\sqrt[]{(6-1)^2+(1-2)^2} \\ AC=\sqrt[]{25+1} \\ AC=\sqrt[]{26} \\ AC\approx5.099\text{units} \end{gathered}`

Therefore, the length of the base is 5.099 units.

Part B:

To get the height of the triangle ABC, the height is BM from the sketch.

Hence, the coordinate of point M is needed.

To get point M which is the midpoint of the line segment AC, we use the formula to get the midpoint.

`\begin{gathered} M=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ \\ \text{where;} \\ x_1=2 \\ x_2=1 \\ y_1=1 \\ y_2=6 \\ \\ \text{Hence,} \\ M=((2+1)/(2),(1+6)/(2)) \\ M=((3)/(2),(7)/(2)) \\ M=(1.5,3.5) \end{gathered}`

Hence, the height BM of the triangle is the distance between points B and M.

Using the distance between two points formula;

`\begin{gathered} d=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ \text{where;} \\ x_1=3 \\ x_2=1.5 \\ y_1=3 \\ y_2=3.5 \\ \\ \text{Hence, } \\ d=BM=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ BM=\sqrt[]{(3.5-3)^2+(1.5-3)^2} \\ BM=\sqrt[]{0.25+2.25} \\ BM=\sqrt[]{2.5} \\ BM\approx1.581\text{units} \end{gathered}`

Therefore, the height of the triangle ABC is 1.581 units