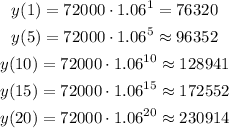Question

After graduating from college, Carlos receives two different job offers. Both pay a starting salary of $72000 per year, but one job promises a $5040 raise per year, while the other guarantees a 6% raise each year. Complete the tables below to determine what his salary will be after t years. Round your answers to the nearest dollar.

Answer 1

The first offer is a linear function.

It starts at y = 72000 for t = 0 and increases 5040 per year, so the slope of the line is m = 5040.

We can model the salary as:

`y=72000+5040\cdot t`

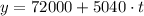
The second offer increases proportionally, so it is an exponential growth.

It increases 6% per year, so the salary at year t is 1.06 times the salary of year (t-1).

We can express it as:

`\begin{gathered} y(0)=72000 \\ y(1)=1.06\cdot y(0)=1.06\cdot72000 \\ y(2)=1.06\cdot y(1)=1.06\cdot1.06\cdot72000=1.06^2\cdot72000 \\ \Rightarrow y(t)=72000\cdot1.06^t \end{gathered}`

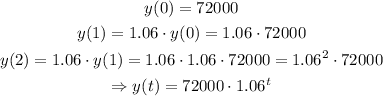
We now can complete the table for the first offer as:

`\begin{gathered} y(1)=72000+5040\cdot1=72000+5040=77040 \\ y(5)=72000+5040\cdot5=72000+25200=97200 \\ y(10)=72000+5040\cdot10=72000+50400=122400 \\ y(15)=72000+5040\cdot15=72000+75600=147600 \\ y(20)=72000+5040\cdot20=72000+100800=172800 \end{gathered}`

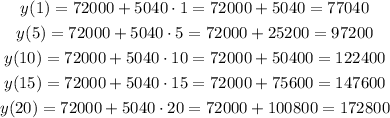
Now, we calculate for the second offer:

`\begin{gathered} y(1)=72000\cdot1.06^1=76320 \\ y(5)=72000\cdot1.06^5\approx96352 \\ y(10)=72000\cdot1.06^(10)\approx128941 \\ y(15)=72000\cdot1.06^(15)\approx172552 \\ y(20)=72000\cdot1.06^(20)\approx230914 \end{gathered}`