Question

The regular hexagon shown below has a perimeter of 30 andcenter C. What is the perimeter of ABC ?

Answer 1

From the statement of the problem, we know that the perimeter of the hexagon in the figure is:

`P_{\text{hexagon}}=30.`

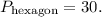
The perimeter is equal to the sum of the lengths of the sides. So each side of the hexagon has a length:

`L_{\text{hexagon}}=(30)/(6)=5.`

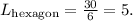
The triangle inscribed in the hexagon is equilateral, so its three sides are equal. We see that the side AB of the triangle is also a side of the hexagon, so we have:

`L_{\text{triangle}}=L_{\text{hexagon}}=5.`

The perimeter of the triangle is equal to the sum of the lengths of its sides, so:

`P_{\text{triangle}}=3\cdot L_{\text{triangle}}=3\cdot5=15.`

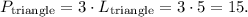
Answer

The perimeter of △ABC is 15.