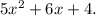Step-by-step explanation
Let's picture the situation of the exercise:
We're looking for the width of the above rectangle. Recall that the area of a rectangle is given by the following equation:
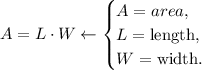
For our rectangle, this equation looks like
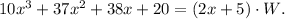
Solving this equation for W, we get
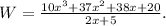
Then, the exercise turns out to be a polynomial division. let's do it:
Then,
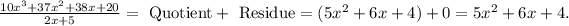
And Thus,
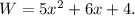
Answer
The width of the given rectangle is