Question

Wildlife biologists treated a pool with a chemical to reduce the amount A of algae. The amount of algae in the pool is given by the function A(t)=35t2-360t+1050 where r is the number of days after treatment.(A)When will the amount of algae reach a minimum?(B)What is the minimum number of algae?(C)How many days after treatment will the amount of algae reach 900?(D)Graph the function.

Answer 1

`A(t)=35t^2-360t+1050`

A

minimum of algae is when we derive and equal 0

Derivation

`\begin{gathered} (2)35t-360 \\ 70t-360 \end{gathered}`

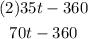
equal 0

`\begin{gathered} 70t-360=0 \\ 70t=360 \\ t=(360)/(70) \\ \\ t=(36)/(7) \end{gathered}`

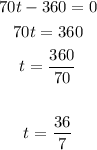
the amout of algae reach minimum when t=36/7

B

to calculate the minumum number of algae we replace the days when algae reach minumum(previus exercise) on function

`\begin{gathered} 35t^2-360t+1050 \\ 35((36)/(7))^2-360((36)/(7))+1050 \\ \\ 35((1296)/(49))-(12960)/(7)+1050 \\ \\ (6480)/(7)-(12960)/(7)+1050 \\ \\ =(870)/(7)\approx124.3 \end{gathered}`

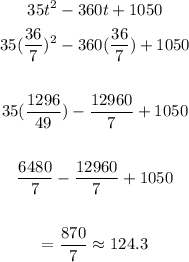
the rounded minimum number of algae is 124

C

We replace the amount of algae to 900 on the original function

`900=35t^2-360t+1050`

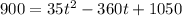
simplify

`\begin{gathered} 35t^2-360t+1050-900=0 \\ 35t^2-360t+150=0 \end{gathered}`

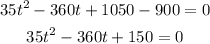
now solve t factoring by

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where x is the variable then t, a is 35, b is -360 and c 150

replacing

`t=\frac{-(-360)\pm\sqrt[]{(-360)^2-4(35)(150)}}{2(35)}`

simplify

`\begin{gathered} t=\frac{360\pm\sqrt[]{129600-21000}}{70} \\ \\ t=\frac{360\pm\sqrt[]{108600}}{70} \\ \\ t=\frac{360\pm\sqrt[]{100*1086}}{70} \\ \\ t=\frac{360\pm10\sqrt[]{1086}}{70} \\ \\ t=\frac{36\pm\sqrt[]{1086}}{7} \end{gathered}`

then the days to have 900 algae is

`\begin{gathered} t_1=\frac{36+\sqrt[]{1086}}{7}\approx9.85 \\ \\ t_2=\frac{36-\sqrt[]{1086}}{7}\approx0.46 \end{gathered}`

we have 2 values for 900 algae 9.85 and 0.46 days

D Graph

we know the graph is a parable because maximum exponent is 2

we know points like,

minimum amount of algae A(5.14 , 124.3) ,

when the amount of algae is 900 B(9.85 , 900) C(0.46 , 900)

then we can palce the points of a graph and join them