Question

If 13 cos Θ = 12 and 180° < Θ < 360 calculate without the use of a calculator A) tan ΘB) (sin Θ + cos Θ)^2

Answer 1

`\begin{gathered} \text{Given} \\ 13\cos \theta=12 \end{gathered}`

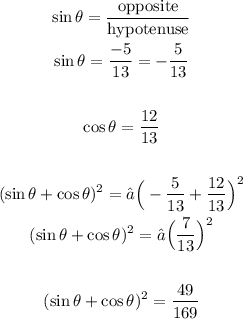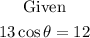
First, solve the given in terms of cos Θ

`\begin{gathered} 13\cos \theta=12 \\ (13\cos \theta)/(13)=(12)/(13) \\ \\ \text{Therefore,} \\ \cos \theta=(12)/(13) \end{gathered}`

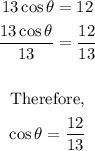
Next, draw a diagram to account for the fact that 180° < Θ < 360°

Solve for the opposite side using Pythagorean Theorem and make the resulting side negative (since it is below in the y-axis as shown on the diagram)

`\begin{gathered} a^2+b^2=c^2 \\ a^2+(12)^2=(13)^2 \\ a^2+144=169 \\ a^2=169-144 \\ a^2=25 \\ \sqrt[]{a^2}=\sqrt[]{25} \\ a=-5 \end{gathered}`

Part A:

Using the information above we can now solve for tan Θ

`\begin{gathered} \tan \theta=\frac{\text{opposite}}{\text{adjacent}} \\ \tan \theta=(-5)/(12) \\ \\ \tan \theta=-(5)/(12) \end{gathered}`

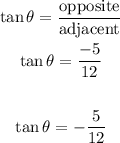
Part B:

`\begin{gathered} \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}} \\ \sin \theta=(-5)/(13)=-(5)/(13) \\ \\ \cos \theta=(12)/(13) \\ \\ \mleft(\sin \theta+\cos \theta\mright)^2=​\Big(-(5)/(13)+(12)/(13)\Big)^2 \\ (\sin \theta+\cos \theta)^2=​\Big((7)/(13)\Big)^2 \\ \\ (\sin \theta+\cos \theta)^2=(49)/(169) \end{gathered}`