Question

Which points are on the plane curve described by the following set of parametric equations? Select all that apply.x=2t+5 and y=3x²

Answer 1

To find:

The point which are on the plane curve.

Solution:

Given parametric equations are x = 2t + 5 and y = 3t^2.

Find the value of t in terms of x.

`\begin{gathered} x=2t+5 \\ x-5=2t \\ (x-5)/(2)=t \end{gathered}`

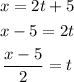
substitute this value of t in y:

`y=3((x-5)/(2))^2`

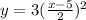
Now, check if every point passes through curve.

at x = 1,

`\begin{gathered} y=3((1-5)/(2))^2 \\ y=3(-2)^2 \\ y=12 \end{gathered}`

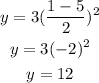
So, the curve does not pass through (1, 7).

at x = 2,

`\begin{gathered} y=3((2-5)/(2))^2 \\ y=3((9)/(4)) \\ y=(27)/(4) \end{gathered}`

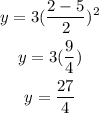
So, the curve does not pass through (2, 9).

at x= 3,

`\begin{gathered} y=3((3-5)/(2))^2 \\ y=3(1)^2 \\ y=3 \end{gathered}`

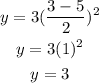
so, the curve does not pass through (3, -3).

at x = 3, y = 3, So, the curve passes through (3, 3).

at x = 7.

`\begin{gathered} y=3((7-5)/(2))^2 \\ y=3(1)^2 \\ y=3 \end{gathered}`

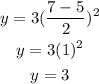
So, the curve passes through (7, 3).

Thus, options D and E are correct.