In a right triangle you use te Pythagorean theoren:
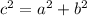
As you have the value of sides b and c, solve the equation fot a:
![\begin{gathered} a^2=c^2-b^2 \\ a=\sqrt[]{c^2-b^2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x83pdjoppx0dcbpg2pm7otyazs9hwgde5v.png)
b= 4
c= 7
![a=\sqrt[]{7^2-4^2}=\sqrt[]{49-16}=\sqrt[]{33}](https://img.qammunity.org/2023/formulas/mathematics/college/ph6lzgv8r8qidihckc7j3o150w5u59baq8.png)
Trigonometric functions for angle B.
Being a the adjacent and b the opposite, c is the hypotenuse. To rationalizing the denominator multiply the fraction by a fraction with the radical in numerator and denominator:
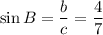
![\cos B=(a)/(c)=\frac{\sqrt[]{33}}{7}](https://img.qammunity.org/2023/formulas/mathematics/college/67czvhp1lmu24pjsjnkmchnawqu719ttln.png)
![\tan B=(b)/(a)=\frac{4}{\sqrt[]{33}}\cdot\frac{\sqrt[]{33}}{\sqrt[]{33}}=\frac{4\cdot\sqrt[]{33}}{33}](https://img.qammunity.org/2023/formulas/mathematics/college/81kp3jkvi0yw8nklchqkcdj6xl301287dn.png)
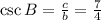
![\sec B=(c)/(a)=\frac{7}{\sqrt[]{33}}\cdot\frac{\sqrt[]{33}}{\sqrt[]{33}}=\frac{7\cdot\sqrt[]{33}}{33}](https://img.qammunity.org/2023/formulas/mathematics/college/abplzekdx0aq6mjoi54n10rbwbsbyblo1c.png)
![\cot B=(a)/(b)=\frac{\sqrt[]{33}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/hy6zga7jet09a70txak9oepo2w872q9xvj.png)