Question

How do I solve and what is the question asking for

Answer 1

First, let's find the tangent line at x = 2

We know that:

`\begin{gathered} f(2)=2^2-2(2)+3 \\ \rightarrow f(2)=3 \end{gathered}`

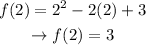
This way, we know that point (2,3) belongs to the line.

For the slope, we know that

`m=f^(\prime)(2)`

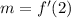
And that

`f^(\prime)(x)=2x-2`

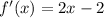
This way,

`\begin{gathered} m=2(2)-2 \\ \Rightarrow m=2 \end{gathered}`

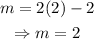
Using this slope, the point we've found and the slope-intercept form, we'll get that the equation of the line is:

`\begin{gathered} y-3=2(x-2) \\ \rightarrow y-3=2x-4 \\ \rightarrow y=2x-4+3 \\ \\ \Rightarrow g(x)=2x-1 \end{gathered}`

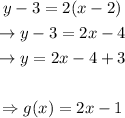
Now for the tricky part: The question states that we must find the greatest value of x in which "... the error resulting in this tangent line aproximation is less than 0.5"

This means that if we find the difference between f(x) and g(x), for any point x, it has to be less than 0.5

`f(x)-g(x)\le0.5`

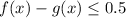
Now, we know that this difference can be either from below or from above (It can be 0.5 or -0.5). Therefore, we must include an absolute value in our condition:

`\begin{gathered} f(x)-g(x)\le0.5 \\ \\ \Rightarrow\lvert f(x)-g(x)\rvert\le0.5 \end{gathered}`

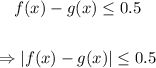
Since we've already defined f(x) and g(x), we can plug them in in this formula and simplify:

`\begin{gathered} \lvert f(x)-g(x)\rvert\le0.5 \\ \rightarrow\lvert(x^2-2x+3)-(2x-1)\rvert\le0.5 \\ \rightarrow\lvert x^2-2x+3-2x+1\rvert\le0.5 \\ \rightarrow\lvert x^2-4x+4\rvert\le0.5 \end{gathered}`

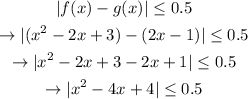
Therefore, we have to find the biggest value of x for which the expression

`\lvert x^2-4x+4\rvert\le0.5`

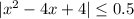
is true.

Let's start from the biggest value in the answer options and work our way down until we find the first x value that satisfies the condition:

`\begin{gathered} x=2.8 \\ \rightarrow\lvert(2.8)^2-4(2.8)+4\rvert\le0.5 \\ \rightarrow0.64\le0.5❌ \\ \\ x=2.7 \\ \rightarrow\lvert(2.7)^2-4(2.7)+4\rvert\le0.5 \\ \rightarrow0.49\le0.5\text{ }✅ \end{gathered}`

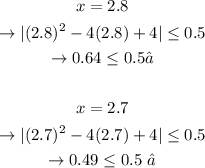
Thereby, we can conclude that the value we're looking for is:

D) 2.7