Question

I need help with this question it’s hard to me

Answer 1

Set x be the amount Roscoe invested in the first account; similarly, y is the amount invested in the second account.

Therefore, the final balance in both accounts is

`\begin{gathered} A_1=x(1+11\%)=x(1+0.11)=x(1.11)=1.11x \\ and \\ A_2=y(1+9\%)=y(1+0.09)=1.09y \end{gathered}`

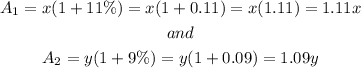
Furthermore, we have that,

`\begin{gathered} x+y=7700 \\ and \\ Total\text{ Interest }=(A_1+A_2)-7700=787 \end{gathered}`

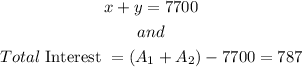
Thus,

`\begin{gathered} \Rightarrow x+y=7700 \\ and \\ 1.11x+1.09y-7700=787 \\ \Rightarrow0.11x+0.09y=787 \end{gathered}`

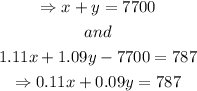
Substituting the first equation into the second one,

`\begin{gathered} \Rightarrow x=7700-y \\ \Rightarrow0.11(7700-y)+0.09y=787 \\ \Rightarrow847-0.11y+0.09y=787 \\ \Rightarrow0.02y=60 \\ \Rightarrow y=(60)/(0.02)=3000 \end{gathered}`

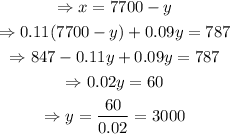
Finding the corresponding value of x,

`\begin{gathered} y=3000 \\ \Rightarrow x=7700-3000=4700 \end{gathered}`

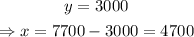
Hence, Roscoe invested $4700 at 11% and $3000 at 9%