Question

* The equilibrium constant, K, for the reaction of NO with Cl2 is 52 at 500 K. 2NO(g) + Cl2(g) 2NOCI(g) The partial pressure of NO and Cl, at equilibrium are 0.240 atm and 0.608 atm respectively. Calculate the partial pressure of NOCI at 500 K.

Answer 1

Explanation:

Firstly, we need to write out the balanced equation of the reaction

`2NO_((g))+Cl_(2(g))\rightarrow2NOCl_((g))`

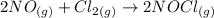
Given parameters

• The equilibrium constant of the reaction = 52

,

• The partial pressure of NO at equilibrium = 0.240 atm

,

• The partial pressure of Cl at equilibrium = 0.608 atm

According to the balanced equation, 2 moles of NO reacts with 1 mole of Cl to give 2 moles of NOCL

The equilibrium constant of the reaction is given below

`k_p\text{ = }\frac{P^2_(NOCL)}{P^2_{NO\text{ }}\cdot P_(Cl)}`

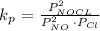
Substituting the parameters into the formula above

`\begin{gathered} 52\text{ = }\frac{P^2_(NOCL)}{(0.240)^2\cdot\text{ 0.608}} \\ 52\text{ = }\frac{P^2_(NOCL)}{0.0576\cdot\text{ 0.608}} \\ 52\text{ = }(P^2_(NOCL))/(0.0350) \\ \text{Cross multiply} \\ 52\cdot0.0350=P^2_(NOCL) \\ 1.821=P^2_(NOCL) \\ \text{Take the square roots of both sides} \\ \sqrt[]{1.821}\text{ = }\sqrt[]{P^2_(NOCL)} \\ P_{NOCL\text{ }}=\text{ }1.350\text{ atm} \end{gathered}`

Hence, the partial pressure of NOCL at 500K is 1.350atm