Question

Use the graph to answers the following 2 questions: 1. Write the equation in
`y = {ab}^(x)`form for this graph. 2. Using th equation from #1, what is the value when x=4?

Answer 1

`y=ab^x`

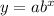
In a equation in the exponential general form you have:

a is the y-intercetp: the value of the function when x is 0)

For the given function the y intercept is (0,5), then

a=5

`y=5b^x`

Use the given point (2,45) to find the value of b

y=45

x=2

`45=5b^2`

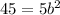
Divide both sides of the equation into 5:

`\begin{gathered} (45)/(5)=(5)/(5)b^2 \\ \\ 9=b^2 \end{gathered}`

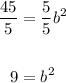
Find the square root in both sides of the equation:

`\begin{gathered} \sqrt[]{9}=\sqrt[]{b^2} \\ \\ 3=b \end{gathered}`

Then, for the given function you have the next equation:

`y=5\cdot3^x`

__________________________________

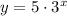
To find the value of the function when x=4 use the equation above, substitute the x for 4 and evaluate:

`\begin{gathered} y=5\cdot3^4 \\ y=5\cdot81 \\ y=405 \end{gathered}`

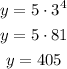
Then, when x=4 the value of the function is 405