Question

Could you please help me? No tutor has been able to answer my question.

Answer 1

The Binomial Probability Distribution states that

`\begin{gathered} Pr(X=k)=(nbinomialk)p^k(1-p)^(n-k) \\ n\rightarrow total\text{ number of trials} \\ k\rightarrow\text{ successful number of trials} \\ p\rightarrow\text{ probability of success} \end{gathered}`

In our case, since the success rate of the vaccine is 92%, its failure rate is equal to 100-92=8%. Then, the Binomial distribution becomes

`P(X=k)=(50binomialk)(0.08)^k(0.92)^(50-k)`

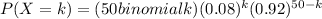
Where we set p=0.08 (probability of the vaccine to fail), and n=50, the 50 patients in the medical practice.

Therefore, we need to find

`\begin{gathered} P(X>1)\rightarrow\text{ probability that the vaccine fails for more than 1 patient} \\ and \\ P(X>1)=1-P(X\leq1) \end{gathered}`

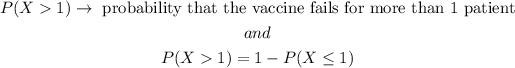
Finding P(X<=1),

`\begin{gathered} P(X\leq1)=P(X=1)+P(X=0) \\ \Rightarrow P(X\leq1)=(50binomial1)(0.08)^1(0.92)^(49)+(50binomial0)(0.08)^0(0.92)^(50) \end{gathered}`

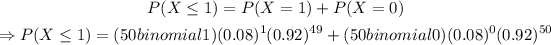
Simplifying,

`\begin{gathered} \Rightarrow P(X\leq1)=50(0.08)(0.92)^(49)+1(1)(0.92)^(50) \\ \Rightarrow P(X>1)=1-50(0.08)(0.92)^(49)-(0.92)^(50) \\ \Rightarrow P(X>1)=0.91729 \end{gathered}`

The rounded answer is 0.91729, the exact answer is the penultimate line above.