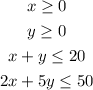Let x be the number of bags of fertilizer and y be the number of bags of peat moss.
If each bag of fertilizer costs $2, if we buy x bags we will have to pay 2x for it.
If each bag of peat moss costs $5, if we buy y bags we will have to pay 5y for it.
In total, we would have to pay 2x + 5y.
Since Jake does not want to spend more than $50 on them, this sum have to be less than or equal to 50, so we have the first inequality of the system:
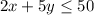
Also, Jake's van can hold at most 20 bags, so if we buy x bags of fertilizer and y bags of peat moss, we will have a total of x + y bags, and this have to be less than of equal to 20, so we have the second inequality of the system:
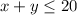
Also, we can't buy a negative number of bags of fertilizer or peat moss, so x and y each must be greater than or equal to 0:
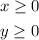
So, the system of inequalities is: