Solution
Firstly, we will find the third angles of both triangles,
The sum of angles in a triangle is 180 degrees.
If we know that two angles of one triangle are 112° and 39°
Let the third angle be x
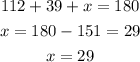
The third angle is 29 degrees
And two angles of another triangle are 39° and 29°
Let the third angle be y
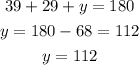
The third angle is 112 degrees
Two triangles are similar if their corresponding angles are equal.
Since, their corresponding angles are equal
Hence, then the two triangles must be similar (option d)