ANSWER
Solving this system for x,
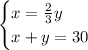
Step-by-step explanation
We have two numbers. Let them be x and y. We know that one of them is 2/3 of the other, so this makes one equation,

And we also know that the sum of these two numbers is 30, so we have another equation,

To find the smaller number we would solve this system for x,
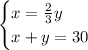
From the first equation, we know that x represents the smaller number.