Let's begin by listing out the information given to us:
Height (h) = 40 ft, diameter (d) = 20 ft, radius (r) = 20/2 = 10 ft
The volume of the tank is given by:
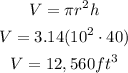
The volume of the tank is given by the product of pi, radius square & the height of the tank
Volume = 3.14 * 10² * 40 = 12,560 ft³
You pick up 4 pumps that can pump half the volume of the tank in 1 hour = 12560/2 ft³/h = 6280 ft³/h
Each pump supplies this amount of water:
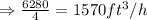
Each pump supplies 1,570 ft³/h of water. If it takes 1 hour to fill half the tank, then it will take 2 hours to fill the tank.
Convering 1570 ft³/h to gal/h, we have:
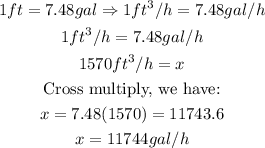
Therefore, each pump supplies 11,744 gallons per hour