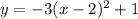Question

What is the vertex form of the quadratic function that has a vertex at (2, 1) and goes through the point (3,-2)?

Answer 1

Given:

There are given the vertex and point :

`\begin{gathered} vertex:(2,1) \\ point:(3,-2) \end{gathered}`

Step-by-step explanation:

According to the question:

We need to find the quadratic function in the form of vertex:

So,

From the vertex form of the equation:

`y=a(x-h)^2+k`

Where,

`\begin{gathered} h=2 \\ k=1 \end{gathered}`

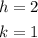
Then,

Put both the value into the given vertex form:

So,

`\begin{gathered} y=a(x-h)^(2)+k \\ y=a(x-2)^2+1...(1) \end{gathered}`

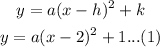
Now,

We need to find the value of a:

So,

Put 3 for x and -2 for y into the equation (1):

Then,

`\begin{gathered} \begin{equation*} y=a(x-2)^2+1 \end{equation*} \\ -2=a(3-2)^2+1 \\ -2=a(1)^2+1 \\ -2=a+1 \\ a=-3 \end{gathered}`

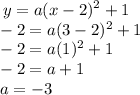
Then,

Put the value of an into the equation (1):

So,

`\begin{gathered} \begin{equation*} y=a(x-2)^2+1 \end{equation*} \\ y=-3(x-2)^2+1 \end{gathered}`

Final answer:

Hence, the vertex form of the quadratic function is shown below:

`y=-3(x-2)^(2)+1`