Given: The mean rate of cars per half an hour is 3
To Determine: The probability that, in any hour, exactly 4 cars will enter the car wash
Solution
The poison formular is given as

Where
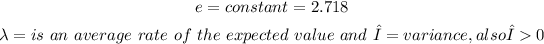
If we have a mean rate of 3 cars per half an hour. Therefore in an hour the mean rate would be 6
So, substituting into the formula
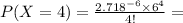
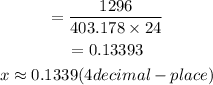
Hence, the probability is approximately 0.1339