Question

Please help this is my third Tudor for this question. Thanks

Answer 1

Given the function below

`f(x)=(5x^2+36x-32)/(x-1)=((5x-4)(x+8))/((x-1))`

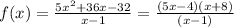
The domain of the function above is the set of input (i.e. x) for the which the function is real and defined.

To achieve this, let us find the undefined points. The function is undefined when the denominator is equal to zero. So the value of x for which the function is undefined is

`\begin{gathered} x-1=0 \\ x=1 \end{gathered}`

If the function is undefined at x = 1, then it will be defined when x is less than x or when x is greater than x (i.e. x < 1, or x > 1). This can be represented in interval notation as

(- ∞, 1) ∪ (1, ∞)

1. Hence, the domain in interval notation is (- ∞, 1) ∪ (1, ∞)

The y intercept is the point where the value of x is zero in the function. This is as shown below:

`\begin{gathered} f(x)=((5x-4)(x+8))/((x-1)) \\ \text{put,x}=0 \\ f(x)=((5(0)-4)(0+8))/((0-1)) \\ f(x)=((0-4)(8))/(-1) \\ f(x)=(-32)/(-1) \\ f(x)=32 \end{gathered}`

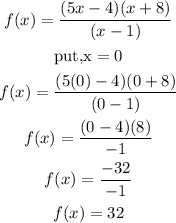
2. Hence, the y - intercept is the point (0, 32)

The x - intercept is the point where the function is equal to zero or where y = 0. This is as shown below:

`\begin{gathered} f(x)=((5x-4)(x+8))/((x-1)) \\ \text{put f(x) = 0} \\ 0=((5x-4)(x+8))/((x-1)) \\ \text{cross}-\text{multiply} \\ (5x-4)(x+8)=0(x-1) \\ (5x-4)(x+8)=0 \\ 5x-4=0,or,x+8=0 \\ 5x=4,or,x=-8 \\ x=(4)/(5),or,x=-8 \end{gathered}`

3. Hence, the x - intercept is the points (4/5, 0) (-8, 0)

The vertical asymptote is calculated by first reducing the function to its least terms as given below

`f(x)=((5x-4)(x+8))/((x-1))`

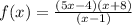
Since the function cannot be divisible further, then we equate the denominator equal zero. So, the vertical asymptote is

`\begin{gathered} x-1=0 \\ x=1 \end{gathered}`

4. Hence, the vertical asyptote is at the point x = 1

The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.

It should be noted that when

1- Degree of numerator is less than degree of denominator: horizontal asymptote at y = 0.

2- Degree of numerator is greater than degree of denominator by one: no horizontal asymptote; slant asymptote.

3- Degree of numerator is equal to degree of denominator: horizontal asymptote at ratio of leading coefficients

From the rational function given below:

`f(x)=(5x^2+36x-32)/(x-1)`

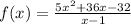
From the above, the degree of the numerator is 2 and that of thenumerator is 1.

The degree of numerator is greater than degree of denominator by one, so there is no horizontal asymptote but a slant asymptote

So the end result of the function would be

`(5x^2)/(x)=5x`

This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function say h(x) = 5x. As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote.

However, the graph of h(x) = 5x looks like a diagonal line, and since f will behave similarly to g, it will approach a line close to h(x) = 5x. This line is a slant asymptote

To get the equatio of the slant asymptote, we will divide the given function to get the quotient and the remainder as shown below:

`(5x^2+36x-32)/(x-1)=(5x+41)+(9)/(x-1)`

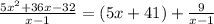
It can be found using long division to divide gives us a quotient of 5x+41, and the remainder is 9. The slant asyptote is the equation of the line of the quotient

5. Hence, the slant asymptote is the equation y= 5x + 41