We are given the point Q and its coordinates. We will first calculate the coordinates of point Q' and then calculate the distance between points Q and Q' using the distance formula.
First we will calculate the coordinates of Q'. We are told that we obtain Q' if we move Q 9 units to the left and the 6 units up. This means that we should take the x coordinate of Q and subtract 9 from it. So we get
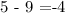
In the same manner, we should add 6 units to the y coordinate of Q. So we get
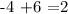
So the coordinates of Q' are ( -4,2).
Now, we want to calculate the distance between this points using the distance formula. Recall that given points (a,b) and (c,d) the distance between these two points is given by the formula
![d=\sqrt[]{(c-a)^2+(d-b)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/r0k3gysy6fz1kxcaiutzg8kz628cbzwkh4.png)
In our case, let us take a= 5, b= -4, c= -4 and d=2. Then the distance would be
![d=\sqrt[]{(-4-5)^2+(2-(-4))^2}=\sqrt[]{(-9)^2+(6)^2}=\sqrt[]{81+36}=\sqrt[]{117}\approx10.8166](https://img.qammunity.org/2023/formulas/mathematics/college/km1o0bfshki5218xd74fotls35qhj65peg.png)
So, the closes whole number to this value is 11.