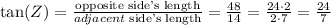Question

Match the correct trig ratios for this triangle: Z 50 14 X 48 Y sin X [Choose] < cos X

Answer 1

Recall that the question is asking us to calculate the sine, cosine and tangent of an angle.

Suppose we have the following triangle

We can define the trigonometric ratios as follows:

The cosine of the angle is the adjacent side's length divided by the length of the hypotenuse, so we have

`\cos (\text{angle)}=(b)/(c)`

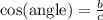
The sine of the angle is the opposite side's length divided by the length of the hypotenuse, so we have

`\sin (\text{angle)}=(a)/(c)`

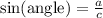
Finally, the tangent of the angle is the opposite side's length divided by the adjacent side's length. So we have

`\tan (\text{angle)=}(a)/(b)`

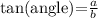
In our case, we want to calculate sin(X) and cos(X) first. So we have the triangle

In this case, we need to identify the opposite and adjacent sides with respect to angle X. We can see from the picture that the opposite side is the one with length 14 and the adjacent side is the one with length 48. This leaves the other side with length 50 as the hypotenuse. So we have, using the previous definitions, that

`\sin (X)=\frac{\text{opposite side's length}}{hypotenuse^(\prime)s\text{ length}}=(14)/(50)=(2\cdot7)/(25\cdot2)=(7)/(25)`

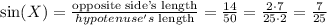
also

`\cos (X)=\frac{\text{adjacent side's length }}{hypotenuse^(\prime)s\text{ length}}=(48)/(50)=(24\cdot2)/(25\cdot2)=(24)/(25)`

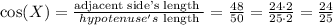
Now, we want to calculate tan(Z). To do so, we want to identify the adjacent and opposite sides with respect to angle Z. We can see from the picture above that the opposite side is the one with length 48 and the adjacent side is the one with length 14. This leaves the hypotenuse as 50.

Using the previous definitions, we have that

`\tan (Z)=\frac{\text{opposite side's length}}{adjacent\text{ side's length}}=(48)/(14)=(24\cdot2)/(2\cdot7)=(24)/(7)`