Question

Find the magnitude of the net gravitational force exerted by the two larger masses on the 56. 1 kg mass. The value of the universal gravi- tational constant is 6.672 x 10 l N m²/kg? Answer in mits of N. 11 017 (part 2 of 2) 10.0 points Leaving the distance between the 210 kg and the 103 kg masses fixed, at what distance from the 403 kg mass (other than infinitely remote ones) does the 56. 1 kg mass experience a net Answer in units of m.

Answer 1

Given data:

* The mass of the first source is,

`m_1=210\text{ kg}`

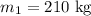
* The mass of the second source is,

`m_2=403\text{ kg}`

* The distance between the sources is,

`d=0.471\text{ m}`

* The mass of the test mass is,

`m=56.4\text{ kg}`

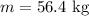
Solution:

Let the distance of test mass from the first source mass be x.

The distance from the second source is,

`D=d-x`

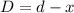
The net force on the test mass is zero if the gravitational force on the test mass due to the first source is equal to the gravitational force on the test mass due to the second source.

Thus,

`\begin{gathered} F_1=F_2 \\ (Gm_1m)/(x^2)=(Gm_2m)/((d-x)^2)^{} \\ (m_1)/(x^2)=(m_2)/((d-x)^2) \end{gathered}`

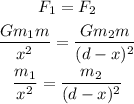
Substituting the known values,

`(210)/(x^2)=(403)/((0.471-x)^2)`

By cross multiplications,

`\begin{gathered} 210(0.471-x)^2=403x^2 \\ (0.471-x^{})^2=1.92x^2 \\ 0.22+x^2-0.94x=1.92x^2 \\ 1.92x^2-x^2+0.94x-0.22=0 \end{gathered}`

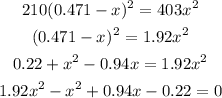
By simplifying,

`0.92x^2+0.94x-0.22=0`

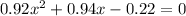
By solving the quadratic equation,