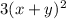Question

3x^2+6xy+3y^2factor completely

Answer 1

So we must factor the following expression:

`3x^2+6xy+3y^2`

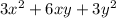
First of all is important to notice that all terms are multiplied by an integer that is a multiple of 3. Then 3 is a common factor and we can re-write the expression like this:

`3x^2+6xy+3y^2=3\cdot(x^2+2xy+y^2)`

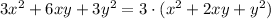
Now let's have a look at the expression inside parenthesis but first let's recall the expression for the square of a binomial. For two real numbers a and b we get:

`(a+b)^2=a^2+2ab+b^2`

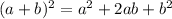
If you replace a and b with x and y we get the following:

`a^2+2ab+b^2\rightarrow x^2+2xy+y^2`

Which means that:

`x^2+2xy+y^2=(x+y)^2`

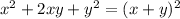
Then the factored form of the original expression and answer to this problem is:

`3(x+y)^2`