To answer this question, we can use trigonometric ratios. We have that the triangle is as follows:
As we can see we need to find the hypotenuse, and we can see that 5 is the opposite side to the angle 45.
We also know that:
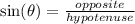
Therefore, we can use this trigonometric ratio to solve this question. Then we have:
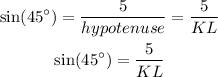
Now, we can multiply both sides by KL as follows:
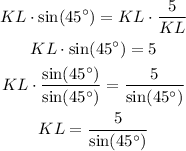
Notice that we also divided both sides by sin(45°). Then we have:
![\begin{gathered} \sin (45^(\circ))=\frac{\sqrt[]{2}}{2} \\ KL=\frac{5}{\frac{\sqrt[]{2}}{2}}\Rightarrow KL=5\cdot\frac{2}{\sqrt[]{2}}=\frac{10}{\sqrt[]{2}}\cdot\frac{\sqrt[]{2}}{\sqrt[]{2}}=\frac{10\sqrt[]{2}}{2}=5\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/g9eefpvstb52ktqzecdrsucin90q3ddpvt.png)