Answer:
h
( - ∞, 12/7 ]
Step-by-step explanation:
To solve the inequality we need to subtract 1 on both sides as:
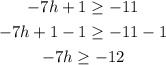
Now, dividing by -7, we get:
Remember that when we multiply or divide by a negative number, the sign of the inequality change, so:
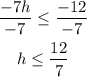
Therefore, the answer in set-builder notation is:
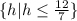
And the answer in interval notation is:
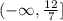
Finally, The answer in a number line is: