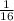Given:
There are four cards numbered as
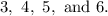
Required:
We have to find the probability of picking a 6 and then picking a 3.
Step-by-step explanation:
When you pick a card at random there are four possibilities.
The possibility of picking a 6 is only one.
Hence the probability of picking a 6 on the first card is
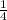
Since you have put back the first card so in the second card there are again four possibilities.
The possibility of picking a 3 is only one.
Hence the probability of picking a 3 on the second card is
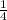
Hence the probability of picking a 6 and then picking a 3 is
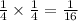
Final answer:
Hence the final answer is