ANSWER
The market equilibrium point is x + 21y
Explanation:
Given information
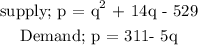
At the market equilibrium, quantity demand is equal to quantity supply
The next step is to equate the two equations together
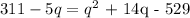
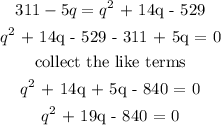
The next process is to solve for q using the general quadratic formula
![\begin{gathered} x\text{ =}\frac{-b\text{ }\pm\sqrt[]{b^2\text{ - 4ac}}}{2a} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/mue381xe6se693r8wsbqq8hgi6i714emt9.png)
Where
a = 1, b = 19 and c = -840
![\begin{gathered} q\text{ =}\frac{-(19)\pm\sqrt[]{19^2-\text{ 4(1 }*-840)}}{2\text{ }*1} \\ q\text{ = }\frac{-19\text{ }\pm\sqrt[]{361\text{ - 4(-840)}}}{2} \\ q\text{ = }\frac{-19\text{ }\pm\sqrt[]{361\text{ + 3360}}}{2} \\ q\text{ = }\frac{-19\pm\sqrt[]{3721}}{2} \\ q\text{ = }(-19\pm61)/(2) \\ q\text{ = }\frac{-19\text{ + 61}}{2}\text{ OR }\frac{-19\text{ - 61}}{2} \\ q\text{ = }(42)/(2)\text{ or }(-80)/(2) \\ q\text{ = 21or -40} \\ q\text{ = 21} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/lbrt0tgh7h8ciniw2ud8psk2dcvqbwuln0.png)
From the above calculations, you will see that the value of q is 21 or - 40
Therefore, the market equilibrium price is 21
Recall that, the general function for the market equilibrium point is
Q(s) = x + yP
where p = price
Hence, the market equilibrium point is q(s) = x + 21y