Question

Please help me solve this(answers need to be rounded to the nearest 10th)

Answer 1

Step 1:

Write all the trigonometric ratio for a right angle triangle

`\begin{gathered} sin\theta\text{ = }(opposite)/(hypotenuse) \\ cos\theta=\frac{adjacent}{\text{hypotenuse}} \\ tan\theta=\frac{\text{oppos}\imaginaryI\text{te}}{adjacent} \end{gathered}`

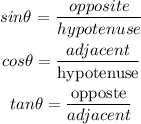
Step 1:

Redraw the diagram and label all its sides.

The side facing the given angle is the opposite = ?

The side facing the right angle is the hypotenuse = 32

The third leg is the adjacent = x

Step3

The cosine ratio will be used to find the value of x since the given sides are adjacent and the hypotenuse.

`\begin{gathered} cos\theta=\text{ }(Adjacent)/(Hypotenuse) \\ cos57\text{ = }(x)/(32) \\ 0.5446\text{ = }(x)/(32) \\ \text{x = 0.5446 }*32 \\ x\text{ = 17.4} \end{gathered}`

Final answer

x = 17.4