Answer:
The gravitational potential energy and kinetic energy of this ball should be equal (assuming that there is no energy loss due to friction.)
Step-by-step explanation:
The ball loses gravitational potential energy as it rolls down the hill. At the same time, the speed of the ball increases, such that the ball gains kinetic energy.
If there is no friction on this ball (and that the ball did not deshape,) all the gravitational potential energy that this ball lost would be converted to kinetic energy.
If the gravitational field strength
 is constant throughout, the gravitational potential energy of an object in that gravitational field would be proportional to its height.
is constant throughout, the gravitational potential energy of an object in that gravitational field would be proportional to its height.
If
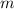 denote the mass of this ball, the gravitational potential energy (
denote the mass of this ball, the gravitational potential energy (
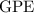 ) of this ball at height
) of this ball at height
 would be
would be
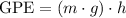 , which is proportional to
, which is proportional to
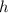 .
.
The value of
 near the surface of the earth is indeed approximately constant (typically
near the surface of the earth is indeed approximately constant (typically
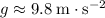 .)
.)
At halfway between the top and bottom of this hill, the height of this ball would be
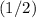 of its initial value (the value when the ball was at the top of the hill.) Because the
of its initial value (the value when the ball was at the top of the hill.) Because the
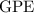 of this ball is proportional to its height, at halfway down the hill, the
of this ball is proportional to its height, at halfway down the hill, the
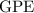 of this ball would also be
of this ball would also be
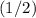 its initial value.
its initial value.
However, if there was no friction on this ball (and that the ball did not deshape,) that
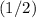 of the initial
of the initial
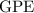 of this ball was not lost. Rather, these
of this ball was not lost. Rather, these
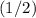 of the initial
of the initial
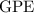 would have been converted to the kinetic energy (
would have been converted to the kinetic energy (
 ) of this ball.
) of this ball.
Hence, when the ball is halfway down the hill:
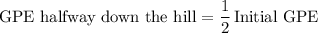 .
.
 .
.
Therefore:
 .
.
In other words, under these assumptions, when this ball is halfway down the hill, the gravitational potential energy and the kinetic energy of this ball would be equal.