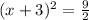Question

Complete the square -2x^2-12x-9=0

Answer 1

Given the Quadratic Equation:

`-2x^2-12x-9=0`

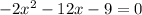
You need to follow these steps in order to complete the square:

1. You can identify that the equation has this form:

`ax^2+bx+c=0`

And, in this case:

`a=-2`

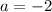
Since you need that:

`a=1`

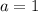
You need to divide both sides of the equation by -2:

`\begin{gathered} -(2x^2)/((-2))-(12x)/((-2))-(9)/((-2))=(0)/((-2)) \\ \\ x^2+6x+(9)/(2)=0 \end{gathered}`

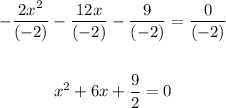
2. Subtract the Constant Term from both sides of the equation:

`\begin{gathered} x^2+6x+(9)/(2)-((9)/(2))=0-((9)/(2)) \\ \\ x^2+6x=-(9)/(2) \end{gathered}`

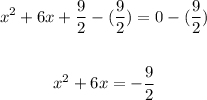
3. Notice that:

`b=6`

You need to add the following value to both sides of the equation:

`((b)/(2))^2=((6)/(2))^2=3^2`

Then:

`\begin{gathered} x^2+6x+3^2=-(9)/(2)+3^2 \\ \\ x^2+6x+3^2=-(9)/(2)+9 \\ \\ x^2+6x+3^2=(9)/(2) \end{gathered}`

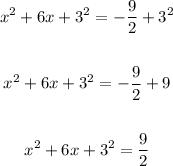
4. Rewrite the Perfect Square on the left side of the equation:

`(x+3)^2=(9)/(2)`

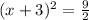
Hence, the answer is:

`(x+3)^2=(9)/(2)`